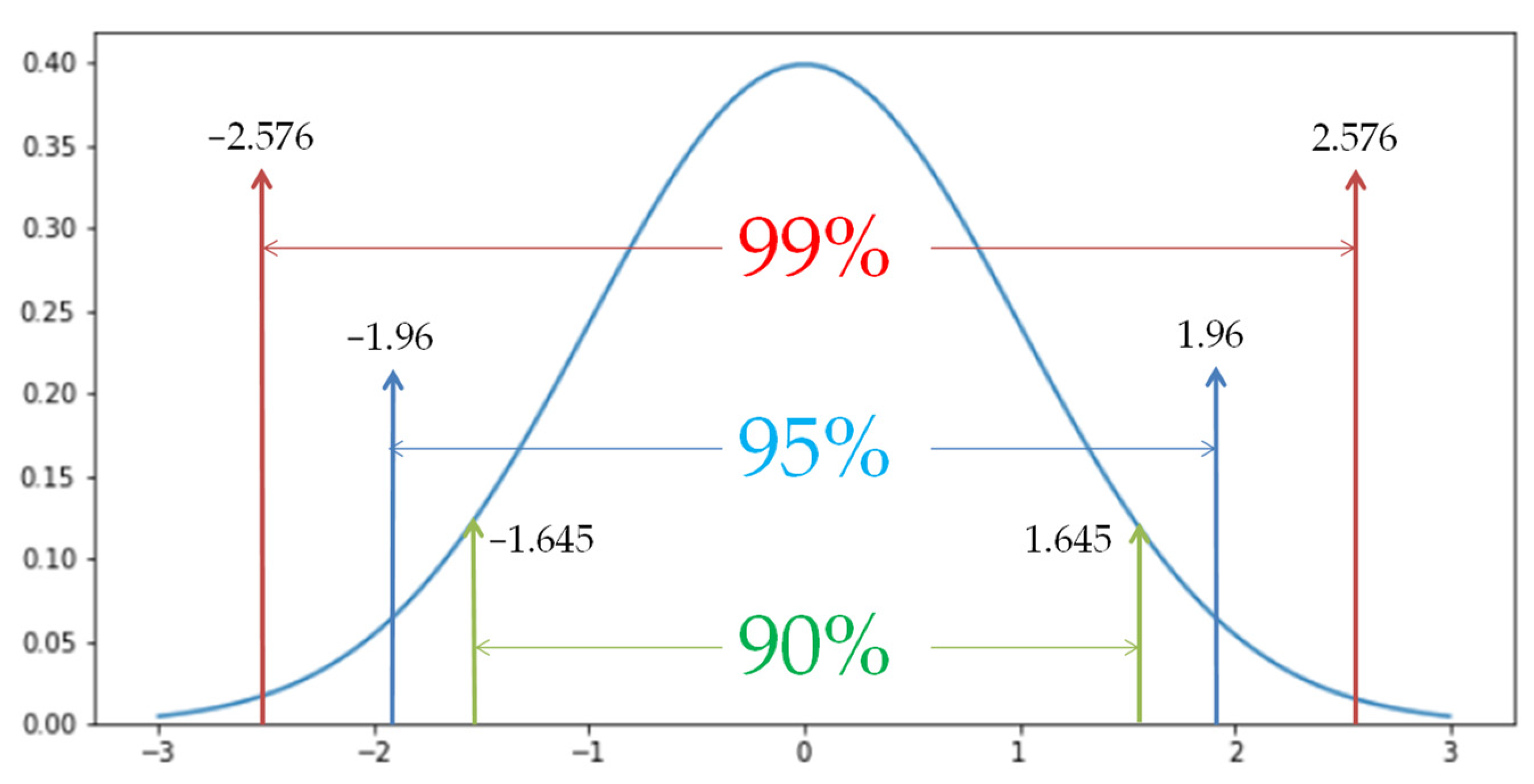
Monte Carlo Simulation Confidence Interval . There are a lot of examples of how to. Monte carlo simulation (or method) is a probabilistic numerical technique used to estimate the outcome of a given, uncertain. The 95% confidence interval is (1.995, 2.585) with the mean of 2.298. This matlab function returns the error probability estimate and 95% confidence interval for a monte carlo simulation of ntrials trials with nerrs errors. In some cases, the random inputs are discrete: (2.10) the central limit theorem can be used to construct confidence intervals for our estimate ˆμn for μ. We want to construct an. For each simulation j j, the. E[f (x )] = f (xi) pi. Confidence intervals represent the inherent variability in the monte carlo simulation by offering a range of likely. X has value xi with probability pi, and then. The coverage probability of the 95% confidence interval for μ μ can also be illustrated using monte carlo simulation.
from www.mdpi.com
The 95% confidence interval is (1.995, 2.585) with the mean of 2.298. This matlab function returns the error probability estimate and 95% confidence interval for a monte carlo simulation of ntrials trials with nerrs errors. The coverage probability of the 95% confidence interval for μ μ can also be illustrated using monte carlo simulation. In some cases, the random inputs are discrete: We want to construct an. Confidence intervals represent the inherent variability in the monte carlo simulation by offering a range of likely. There are a lot of examples of how to. Monte carlo simulation (or method) is a probabilistic numerical technique used to estimate the outcome of a given, uncertain. X has value xi with probability pi, and then. For each simulation j j, the.
Mathematics Free FullText Application of Monte Carlo Simulation to
Monte Carlo Simulation Confidence Interval E[f (x )] = f (xi) pi. We want to construct an. Confidence intervals represent the inherent variability in the monte carlo simulation by offering a range of likely. The coverage probability of the 95% confidence interval for μ μ can also be illustrated using monte carlo simulation. There are a lot of examples of how to. X has value xi with probability pi, and then. The 95% confidence interval is (1.995, 2.585) with the mean of 2.298. For each simulation j j, the. E[f (x )] = f (xi) pi. This matlab function returns the error probability estimate and 95% confidence interval for a monte carlo simulation of ntrials trials with nerrs errors. Monte carlo simulation (or method) is a probabilistic numerical technique used to estimate the outcome of a given, uncertain. (2.10) the central limit theorem can be used to construct confidence intervals for our estimate ˆμn for μ. In some cases, the random inputs are discrete:
From www.researchgate.net
Confidence interval car kilometers traveled per year results Monte Monte Carlo Simulation Confidence Interval The 95% confidence interval is (1.995, 2.585) with the mean of 2.298. E[f (x )] = f (xi) pi. Monte carlo simulation (or method) is a probabilistic numerical technique used to estimate the outcome of a given, uncertain. Confidence intervals represent the inherent variability in the monte carlo simulation by offering a range of likely. For each simulation j j,. Monte Carlo Simulation Confidence Interval.
From www.researchgate.net
llustration of significance and confidence.110Monte Carlo simulations Monte Carlo Simulation Confidence Interval There are a lot of examples of how to. We want to construct an. For each simulation j j, the. Monte carlo simulation (or method) is a probabilistic numerical technique used to estimate the outcome of a given, uncertain. X has value xi with probability pi, and then. This matlab function returns the error probability estimate and 95% confidence interval. Monte Carlo Simulation Confidence Interval.
From www.real-statistics.com
Monte Carlo Simulation Real Statistics Using Excel Monte Carlo Simulation Confidence Interval X has value xi with probability pi, and then. In some cases, the random inputs are discrete: There are a lot of examples of how to. The 95% confidence interval is (1.995, 2.585) with the mean of 2.298. The coverage probability of the 95% confidence interval for μ μ can also be illustrated using monte carlo simulation. (2.10) the central. Monte Carlo Simulation Confidence Interval.
From bookdown.org
7.6 Using Monte Carlo Simulation to Understand the Statistical Monte Carlo Simulation Confidence Interval In some cases, the random inputs are discrete: X has value xi with probability pi, and then. E[f (x )] = f (xi) pi. (2.10) the central limit theorem can be used to construct confidence intervals for our estimate ˆμn for μ. The coverage probability of the 95% confidence interval for μ μ can also be illustrated using monte carlo. Monte Carlo Simulation Confidence Interval.
From www.researchgate.net
Confidence interval at 95 of 1000 sampling of MonteCarlo simulation Monte Carlo Simulation Confidence Interval Monte carlo simulation (or method) is a probabilistic numerical technique used to estimate the outcome of a given, uncertain. The 95% confidence interval is (1.995, 2.585) with the mean of 2.298. The coverage probability of the 95% confidence interval for μ μ can also be illustrated using monte carlo simulation. Confidence intervals represent the inherent variability in the monte carlo. Monte Carlo Simulation Confidence Interval.
From www.elsevier.es
Using the Monte Carlo Simulation Methods in Gauge Repeatability and Monte Carlo Simulation Confidence Interval In some cases, the random inputs are discrete: The 95% confidence interval is (1.995, 2.585) with the mean of 2.298. There are a lot of examples of how to. Confidence intervals represent the inherent variability in the monte carlo simulation by offering a range of likely. This matlab function returns the error probability estimate and 95% confidence interval for a. Monte Carlo Simulation Confidence Interval.
From www.numerade.com
SOLVED Section 2 Confidence Interval (25 Points) 2 The table below Monte Carlo Simulation Confidence Interval X has value xi with probability pi, and then. The 95% confidence interval is (1.995, 2.585) with the mean of 2.298. Monte carlo simulation (or method) is a probabilistic numerical technique used to estimate the outcome of a given, uncertain. E[f (x )] = f (xi) pi. (2.10) the central limit theorem can be used to construct confidence intervals for. Monte Carlo Simulation Confidence Interval.
From www.researchgate.net
Monte Carlo confidence intervals Download Scientific Diagram Monte Carlo Simulation Confidence Interval For each simulation j j, the. Monte carlo simulation (or method) is a probabilistic numerical technique used to estimate the outcome of a given, uncertain. There are a lot of examples of how to. Confidence intervals represent the inherent variability in the monte carlo simulation by offering a range of likely. This matlab function returns the error probability estimate and. Monte Carlo Simulation Confidence Interval.
From www.researchgate.net
Confidence interval at 95 of 1000 sampling of MonteCarlo simulation Monte Carlo Simulation Confidence Interval In some cases, the random inputs are discrete: (2.10) the central limit theorem can be used to construct confidence intervals for our estimate ˆμn for μ. We want to construct an. For each simulation j j, the. Monte carlo simulation (or method) is a probabilistic numerical technique used to estimate the outcome of a given, uncertain. Confidence intervals represent the. Monte Carlo Simulation Confidence Interval.
From www.mdpi.com
Mathematics Free FullText Application of Monte Carlo Simulation to Monte Carlo Simulation Confidence Interval This matlab function returns the error probability estimate and 95% confidence interval for a monte carlo simulation of ntrials trials with nerrs errors. Confidence intervals represent the inherent variability in the monte carlo simulation by offering a range of likely. For each simulation j j, the. E[f (x )] = f (xi) pi. X has value xi with probability pi,. Monte Carlo Simulation Confidence Interval.
From www.ncbi.nlm.nih.gov
Fig. 3.5, Confidence area of the model parameters based on a Monte Monte Carlo Simulation Confidence Interval X has value xi with probability pi, and then. The coverage probability of the 95% confidence interval for μ μ can also be illustrated using monte carlo simulation. Monte carlo simulation (or method) is a probabilistic numerical technique used to estimate the outcome of a given, uncertain. E[f (x )] = f (xi) pi. This matlab function returns the error. Monte Carlo Simulation Confidence Interval.
From www.frontiersin.org
Frontiers Comparison of Bootstrap Confidence Interval Methods for Monte Carlo Simulation Confidence Interval (2.10) the central limit theorem can be used to construct confidence intervals for our estimate ˆμn for μ. The coverage probability of the 95% confidence interval for μ μ can also be illustrated using monte carlo simulation. X has value xi with probability pi, and then. This matlab function returns the error probability estimate and 95% confidence interval for a. Monte Carlo Simulation Confidence Interval.
From www.frontiersin.org
Frontiers Monte Carlo Simulations for the Analysis of Monte Carlo Simulation Confidence Interval E[f (x )] = f (xi) pi. The coverage probability of the 95% confidence interval for μ μ can also be illustrated using monte carlo simulation. The 95% confidence interval is (1.995, 2.585) with the mean of 2.298. X has value xi with probability pi, and then. We want to construct an. (2.10) the central limit theorem can be used. Monte Carlo Simulation Confidence Interval.
From www.scribd.com
Monte Carlo Simulation Using Excel For Predicting PDF Monte Carlo Simulation Confidence Interval There are a lot of examples of how to. Confidence intervals represent the inherent variability in the monte carlo simulation by offering a range of likely. E[f (x )] = f (xi) pi. We want to construct an. For each simulation j j, the. Monte carlo simulation (or method) is a probabilistic numerical technique used to estimate the outcome of. Monte Carlo Simulation Confidence Interval.
From www.buildalpha.com
Monte Carlo Simulation Complete Guide and Simulator Monte Carlo Simulation Confidence Interval In some cases, the random inputs are discrete: Monte carlo simulation (or method) is a probabilistic numerical technique used to estimate the outcome of a given, uncertain. The coverage probability of the 95% confidence interval for μ μ can also be illustrated using monte carlo simulation. E[f (x )] = f (xi) pi. We want to construct an. This matlab. Monte Carlo Simulation Confidence Interval.
From www.researchgate.net
Confidence interval car kilometers traveled per year results Monte Monte Carlo Simulation Confidence Interval The 95% confidence interval is (1.995, 2.585) with the mean of 2.298. Confidence intervals represent the inherent variability in the monte carlo simulation by offering a range of likely. In some cases, the random inputs are discrete: The coverage probability of the 95% confidence interval for μ μ can also be illustrated using monte carlo simulation. We want to construct. Monte Carlo Simulation Confidence Interval.
From www.researchgate.net
Perexposure risk (median ± 95 confidence interval via Monte Carlo Monte Carlo Simulation Confidence Interval There are a lot of examples of how to. The coverage probability of the 95% confidence interval for μ μ can also be illustrated using monte carlo simulation. This matlab function returns the error probability estimate and 95% confidence interval for a monte carlo simulation of ntrials trials with nerrs errors. In some cases, the random inputs are discrete: Confidence. Monte Carlo Simulation Confidence Interval.
From www.researchgate.net
Perexposure risk (median ± 95 confidence interval via Monte Carlo Monte Carlo Simulation Confidence Interval Confidence intervals represent the inherent variability in the monte carlo simulation by offering a range of likely. The 95% confidence interval is (1.995, 2.585) with the mean of 2.298. Monte carlo simulation (or method) is a probabilistic numerical technique used to estimate the outcome of a given, uncertain. E[f (x )] = f (xi) pi. There are a lot of. Monte Carlo Simulation Confidence Interval.